Rule of 72 - the fast and easy way to calculate compound interest

What is the Rule of 72?

I love the Rule of 72, because it's a quick and easy way to estimate the number of years required to double the invested money at a given average annual rate of return.

There are plenty of calculators and spreadsheets that do this for you but the Rule of 72 comes in handy for quick mental calculations. This is the way I roughly calculate all my compound interest equations.

The formula of the Rule of 72

Years to Double = 72 / Interest Rate

AND vice versa

Interest rate (needed) = 72 / Years to Double (desired)

The Rule of 72 applies to anything that grows at a compounded rate, such as population, economic numbers, charges, loans, and my favourite investments!

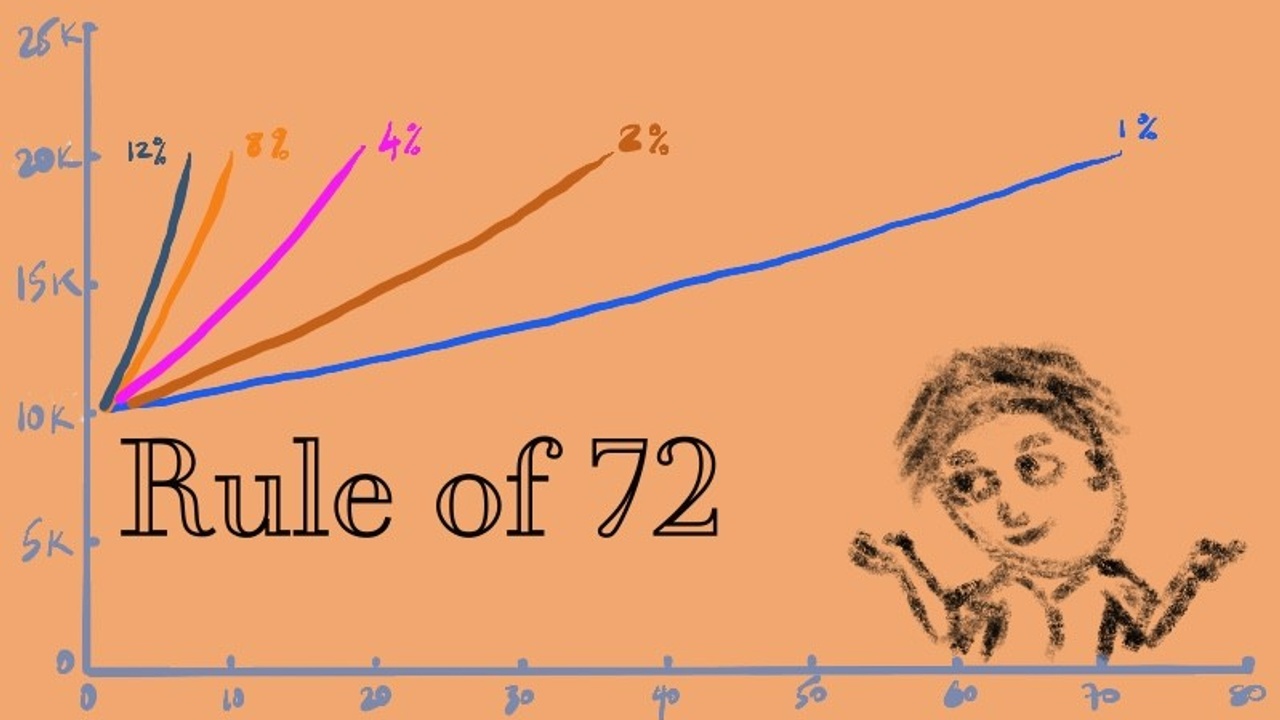
Regarding investing, if you have a fund (or shares) that grows at 4% annually, the initial investment will be expected to double in 72 / 4 = 18 years.

If you are a borrower who pays 20% interest on their credit card (or any other form of loan that is charging interest), then it will double the amount they owe in ~3.5 years!

The rule can also be used to find the amount of time it takes for money's value to halve due to inflation. If inflation is 6%, then a given purchasing power of the money will be worth half in around 12 years (72 / 6 = 12). If inflation decreases from 6% to 4%, then purchasing power is expected to lose half its value in 18 years, instead of 12 years.

Additionally, the Rule of 72 can be applied across multiple durations provided the rate of return is compounded annually. If the interest per quarter is 4%, then it will take (72 / 4) = 18 quarters or 4.5 years to double the principal. If the population of a nation increases at the rate of 1% per month, it will double in 72 months, or six years.

How accurate is the Rule of 72?

The Rule of 72 formula gives you a rough estimate because it is a simplistic equation. It works very well for me because I love round numbers anyway.

AND so many variables go into rates of return and initial principals.

For example, on my investments I calculate that I will get an average annual return of 10% over the long term. Meaning my investments will double every ~7.2 years (72 / 10 = 7.2). Some years will be more and some years it will be less but on average it will be around 10%. Also, I will contribute more to the fund over time which increases the balance.

To continue this example (and my assumptions), I believe my money will double every 7 years. In my retirement accounts, I currently have ~$400,000 and get access to these accounts without penalty 30 years from now. Meaning my investment of $400,000 (today) will double 4 times (there are 4 periods of 7 years within those 30 years). 

The results are:

• $400,000 doubled to $800,000
• $800k doubled to $1.6M
• $1.6M to $3.2M
• $3.2M to $6.4M

Without me adding anything else to my retirement accounts, I will be a multi-millionaire by the time I hit retirement age.

If you don't like these assumptions, then keep the money in longer to get the same ending balance and/or contribute more money to the investment. The results will be roughly the same! AND much better than those of you that don't take action.